Algebra Word Problems

Overview

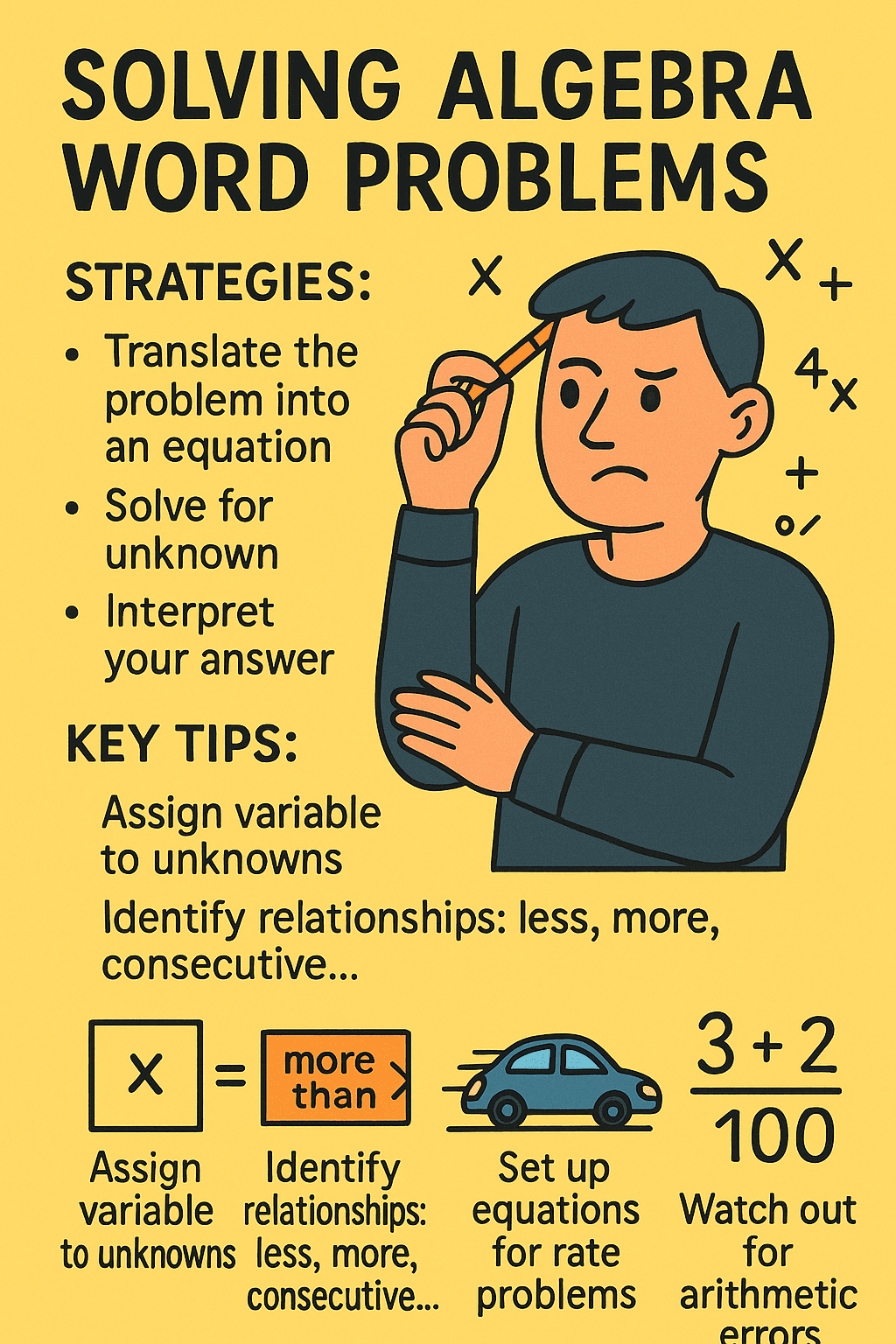
Welcome to this deep-dive on solving algebra word problems! By the end of this article, you'll have a toolkit of strategies for translating real-world situations into algebraic equations, solving for unknowns, and interpreting your answers. We'll break down classic problem types—like age puzzles, speed and distance scenarios, and consecutive integers—so you can confidently tackle similar questions on exams. Expect clear frameworks, practical reasoning steps, and tips to avoid common mistakes.

Concept-by-Concept Deep Dive

Translating Word Problems into Equations

Word problems in algebra require you to bridge the gap between real-life language and mathematical symbols. This skill is foundational: you must identify unknowns, assign variables, and express relationships as equations.

Key Steps:

• Assign Variables: Choose variables to represent unknowns. For example, let $x$ stand for the number of girls in a class or the price of a pen.
• Identify Relationships: Read for phrases like “more than,” “less than,” “twice as,” or “consecutive,” which show how variables are connected.
• Write Equations: Turn the relationships into algebraic expressions. For example, “five more boys than girls” becomes $x = y + 5$.

Misconception Fix:

A common error is misreading relationships—such as swapping "more than" and "less than"—which leads to incorrect equations. Carefully map each phrase before writing.

Solving Systems of Linear Equations

Many word problems involve two (or more) unknowns and relationships, requiring you to solve a system of equations.

Components:

• Set Up the Equations: Based on the problem context, write two equations using the assigned variables.
• Solve by Substitution or Elimination: Plug one equation into the other or add/subtract equations to eliminate a variable.
• Check for Extraneous or Negative Results: Ensure your solution makes sense in context (e.g., negative ages are not valid).

Example Calculation Recipe:

1. Assign variables.
2. Write both equations.
3. Rearrange one equation if needed.
4. Substitute or eliminate to solve for one variable.
5. Plug back in to find the other.

Common Misconception:

Forgetting to check both equations with your candidate solution or misaligning variables with their real-world meaning.

Rate Problems: Distance, Speed, and Time

These classic problems are about objects moving at certain speeds and covering distances within given times.

Key Formula:

• Distance = Speed × Time

Variations:

• Catch-Up Problems: When one object starts later or moves faster—set up equations for both, equate their distances, and solve for time.

Calculation Steps:

1. Define variables for unknown times or distances.
2. Express each object's distance in terms of the variable.
3. Set their distances equal when they “meet” or “catch up.”