Algebra Word Problems

Overview

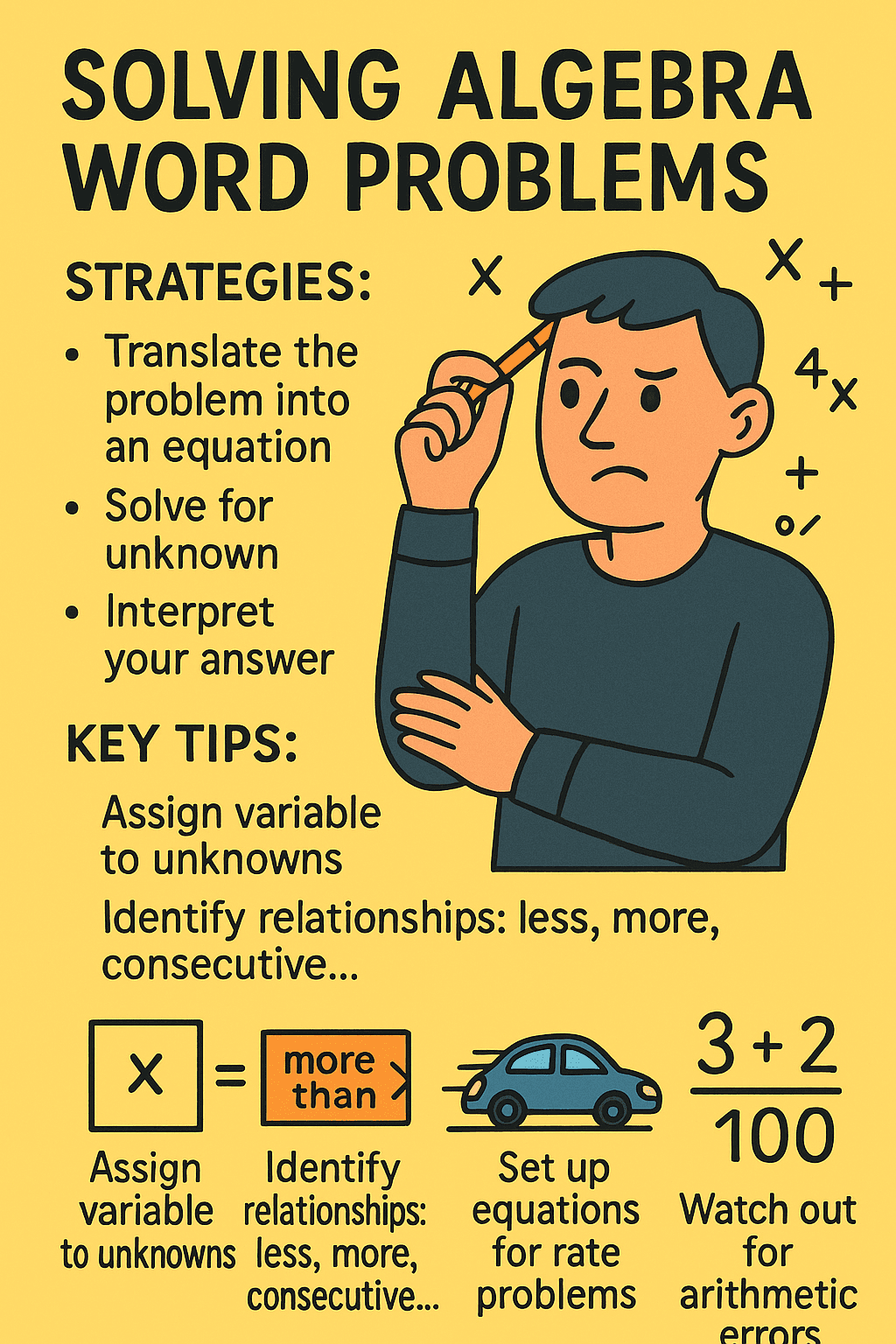
Welcome to this deep-dive on solving algebra word problems! By the end of this article, you'll have a toolkit of strategies for translating real-world situations into algebraic equations, solving for unknowns, and interpreting your answers. We'll break down classic problem types—like age puzzles, speed and distance scenarios, and consecutive integers—so you can confidently tackle similar questions on exams. Expect clear frameworks, practical reasoning steps, and tips to avoid common mistakes.

Concept-by-Concept Deep Dive

Translating Word Problems into Equations

Word problems in algebra require you to bridge the gap between real-life language and mathematical symbols. This skill is foundational: you must identify unknowns, assign variables, and express relationships as equations.

Key Steps:

• Assign Variables: Choose variables to represent unknowns. For example, let $x$ stand for the number of girls in a class or the price of a pen.
• Identify Relationships: Read for phrases like “more than,” “less than,” “twice as,” or “consecutive,” which show how variables are connected.
• Write Equations: Turn the relationships into algebraic expressions. For example, “five more boys than girls” becomes $x = y + 5$.

Misconception Fix:

A common error is misreading relationships—such as swapping "more than" and "less than"—which leads to incorrect equations. Carefully map each phrase before writing.

Solving Systems of Linear Equations

Many word problems involve two (or more) unknowns and relationships, requiring you to solve a system of equations.

Components:

• Set Up the Equations: Based on the problem context, write two equations using the assigned variables.
• Solve by Substitution or Elimination: Plug one equation into the other or add/subtract equations to eliminate a variable.
• Check for Extraneous or Negative Results: Ensure your solution makes sense in context (e.g., negative ages are not valid).

Example Calculation Recipe:

1. Assign variables.
2. Write both equations.
3. Rearrange one equation if needed.
4. Substitute or eliminate to solve for one variable.
5. Plug back in to find the other.

Common Misconception:

Forgetting to check both equations with your candidate solution or misaligning variables with their real-world meaning.

Rate Problems: Distance, Speed, and Time

These classic problems are about objects moving at certain speeds and covering distances within given times.

Key Formula:

• Distance = Speed × Time

Variations:

• Catch-Up Problems: When one object starts later or moves faster—set up equations for both, equate their distances, and solve for time.

Calculation Steps:

1. Define variables for unknown times or distances.
2. Express each object's distance in terms of the variable.
3. Set their distances equal when they “meet” or “catch up.”
4. Solve for the unknown.

Pitfall:

Mixing up who started first or which variable relates to which object.

Consecutive Integers and Patterns

Problems about consecutive numbers (especially odds or evens) are common.

Structure:

• Let the smallest integer be $x$; the next is $x+2$ (for odd/even), and so on.
• Write their sum or product as described.
• Solve for $x$, then find the others.

Tip:

Remember that consecutive odd or even integers differ by 2, not 1.

Proportional and Multiplicative Relationships

Many problems involve ratios like “three times as many” or “gets two more free.”

Typical Steps:

• Assign variables to the basic unit (e.g., number of pens).
• Express the related quantity (e.g., notebooks) as a multiple (e.g., $3x$).
• Use total given to set up your equation.

Example Misconception:

Mixing up which variable refers to which quantity, especially when both are unknown.

Handling Allowance and Spending Problems

Questions may ask about splitting a total into fractional parts and a remainder.

Breakdown:

• Assign variable to the total (e.g., allowance).
• Write expressions for each portion (“half on books” = $\frac{1}{2}x$).
• The remainder is what’s left after subtracting the parts from the total.
• Set up and solve the equation.

Caution:

Be sure all parts add up exactly to the total given.

Price and Purchase Problems

When given bundle purchases and partial information, set up equations for unknown prices or quantities.

Steps:

1. Assign variables to unknown prices or numbers.
2. Multiply quantities by their prices for each category.
3. Add to equal the total spent.
4. Solve for the unknown.

Common Error:

Not matching the quantities and their respective costs correctly.

Worked Examples (generic)

Example 1: Catch-Up Problem

Setup: A bus leaves a station at 50 km/h. Another bus leaves two hours later at 70 km/h. How long until the second bus catches up?

Process:

• Let $t$ = time the second bus travels.
• Distance by first bus: $50(t+2)$.
• Distance by second bus: $70t$.
• At catch-up: $70t = 50(t+2)$.
• Solve for $t$.

Example 2: Consecutive Odd Integers

Setup: The sum of three consecutive odd numbers is 45. What is the largest?

Process:

• Let the smallest be $x$; so next are $x+2$, $x+4$.
• $x + (x+2) + (x+4) = 45$.
• Solve for $x$, then add 4 to get largest.

Example 3: System of Equations (Classroom)

Setup: There are $x$ boys and $y$ girls. There are 7 more boys than girls. Total students is 40.

Process:

• $x = y + 7$
• $x + y = 40$
• Substitute first into second: $(y+7) + y = 40$.
• Solve for $y$.

Example 4: Price Breakdown

Setup: A student buys 4 books at $20 each and 2 pens. Total bill is$100. Find the price of each pen.

Process:

• Let pen price be $x$.
• Total cost: $4 \times 20 + 2x = 100$.
• Solve for $x$.

Common Pitfalls and Fixes

• Mismatched Variables: Assign each variable clearly; double-check what each represents.
• Equation Setup Errors: Translate relationships correctly—especially with "more than" or "less than."
• Ignoring Units: Always track whether answers should be in hours, km, USD, etc.
• Forgetting to Answer the Actual Question: Some problems ask for the largest or smallest value, not the base variable.
• Not Checking Solutions in Context: Plug your answers back in to ensure they make sense in the real scenario.
• Arithmetic Errors: Be meticulous with basic calculations, especially with decimals and fractions.

Summary

• Carefully define variables and translate word problem phrases into algebraic equations.
• For systems of equations, substitute or eliminate to find unknowns, then check your results.
• Use the correct formula for rate/distance/time problems and ensure all time/distance units match.
• For consecutive integer problems, remember the integer differences (1 for general, 2 for odd/even).
• Double-check your arithmetic and ensure your final answer answers the right question.
• Always interpret your solution in the context of the word problem for realism and correctness.