QuizAIMentor

Overview

Welcome to this deep dive into foundational geometry! In this session, you'll develop a clear, practical grasp of key geometric ideas: circles and their properties, converting units, classifying triangles by sides and angles, essential theorems (especially for right triangles), and calculating perimeter and area for basic shapes. By the end, you'll be able to recognize patterns, approach geometry problems with confidence, and avoid the most common errors.

Concept-by-Concept Deep Dive

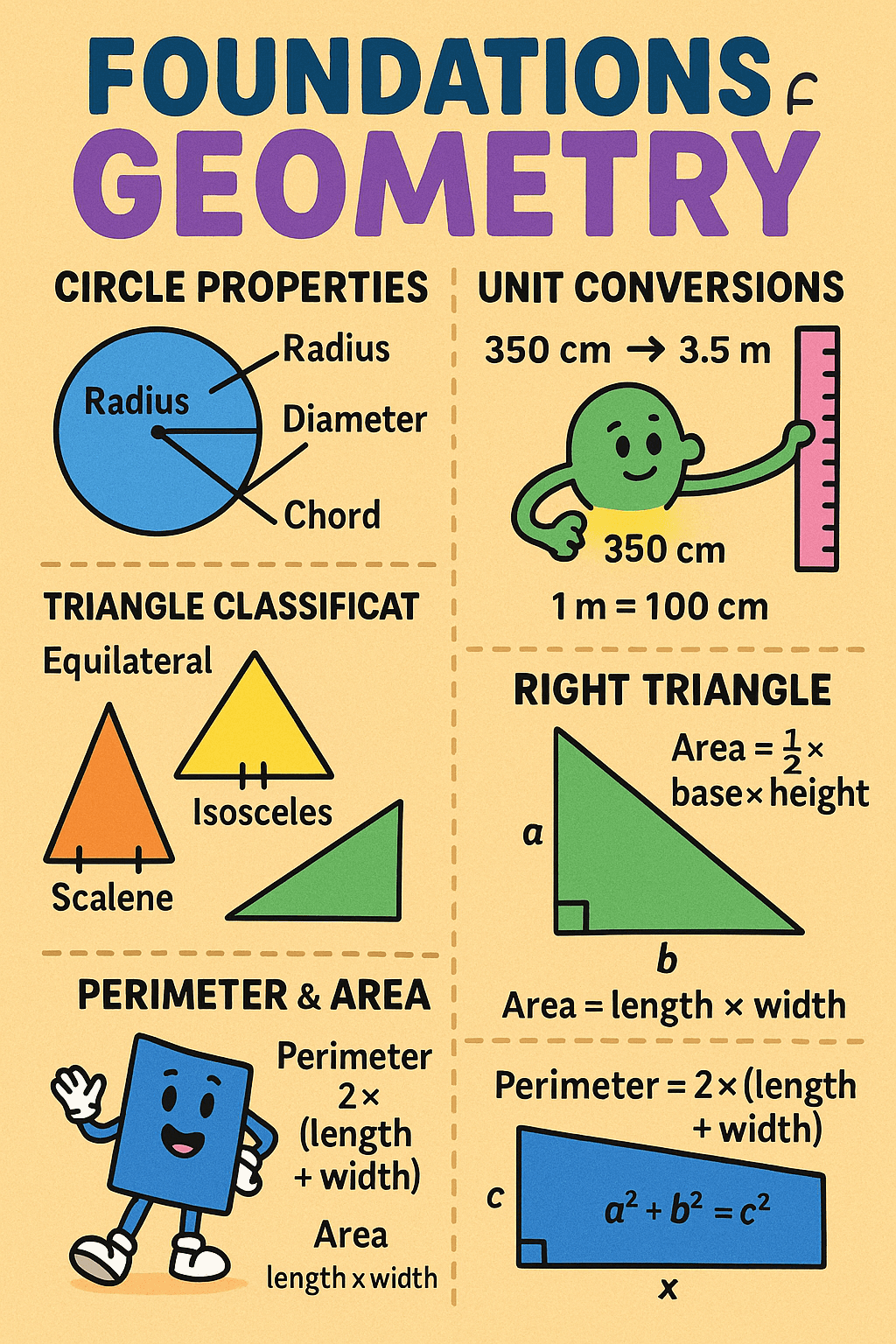
1. Circle Properties: Radius, Diameter, Tangent, and Chord

Circles are defined by all points equidistant from a center. Several core terms—radius, diameter, tangent, and chord—are essential for solving circle problems.

Radius and Diameter

Radius is the distance from the center to any point on the circle.
Diameter is a line passing through the center, touching two points on the circle—twice the radius.
Conversion: If you know one, you can always find the other using the relationship: $\text{Diameter} = 2 \times \text{Radius}$ $\text{Radius} = \frac{\text{Diameter}}{2}$

Tangents

A tangent is a straight line that touches a circle at exactly one point.
Key property: At the point of contact, the tangent is always perpendicular to the radius drawn to that point.
Common misconceptions: Some think a tangent can cross the circle, but it never does; it only touches at a single point.

Chord Length (not passing through the center)

A chord is a straight line joining two points on a circle but not necessarily passing through the center.
If you know the distance from the center to the chord (let's call it $d$ ) and the radius ( $r$ ), you can use the Pythagorean Theorem: $\text{Half chord length} = \sqrt{r^2 - d^2}$ Then, double this to get the full chord length.

2. Unit Conversions

In geometry, measurements are often given in different units. A common task is converting centimeters (cm) to meters (m), or vice versa.

1 meter = 100 centimeters
To convert from centimeters to meters, divide by 100.
To convert from meters to centimeters, multiply by 100.
Example: 350 cm = 3.5 m

Pitfall: Forgetting to divide or multiply by 100, or confusing which way to convert.

3. Triangle Classification and Properties

Triangles are classified by their angles and their side lengths.

By Angles

Right triangle: One angle is exactly 90°.
Acute triangle: All angles less than 90°.
Obtuse triangle: One angle greater than 90°.
Isosceles right triangle: Two angles are equal (45°, 45°, 90°).

By Sides

Equilateral: All three sides equal.
Isosceles: Two sides equal.
Scalene: All sides of different lengths.

Area of a Triangle

For a right triangle: $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$
- The two legs adjacent to the right angle serve as base and height.

Pythagorean Theorem

Applies to right triangles: $a^2 + b^2 = c^2$ where $c$ is the hypotenuse.
Use this to solve for an unknown side.

4. Perimeter and Area of Plane Figures

Rectangle

Perimeter: $\text{Perimeter} = 2 \times (\text{length} + \text{width})$
Area: $\text{Area} = \text{length} \times \text{width}$

Circle

Area: $\text{Area} = \pi r^2$
- Here, $\pi$ is typically approximated as 3.14, and $r$ is the radius.

5. Applying Theorems to Solve Problems

Many geometry problems require combining properties, such as using the Pythagorean theorem for chords and triangles, or understanding how tangents relate to radii.

Step-by-step approach:
1. Identify what is given and what is required.
2. Recall the relevant formula or property.
3. Substitute known values symbolically.
4. Solve algebraically before plugging in numbers.
Common misconceptions: Forgetting to square or take square roots when using the Pythagorean theorem, or misidentifying which sides are base and height in area calculations.

Worked Examples (generic)

Example 1: Finding the Radius from Diameter

A circle has a diameter of $d$ units. To find the radius ( $r$ ):

r = \frac{d}{2}

If $d = 20$ units, then $r = 10$ units.

Example 2: Area of a Right Triangle

A right triangle has legs of length $a$ and $b$ .

\text{Area} = \frac{1}{2}ab

If $a = 6$ units and $b = 8$ units:

\text{Area} = \frac{1}{2} \times 6 \times 8 = 24 \text{ units}^2

Example 3: Converting Centimeters to Meters

Given a length of $L$ cm, to convert to meters:

L_{\text{meters}} = \frac{L}{100}

If $L = 250$ cm, then $L_{\text{meters}} = 2.5$ m.

Example 4: Length of a Chord

A chord is $d$ units from the center of a circle with radius $r$ .

\text{Half chord} = \sqrt{r^2 - d^2}

Full chord $= 2 \times \sqrt{r^2 - d^2}$ .

If $r = 13$ , $d = 5$ :

\text{Half chord} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12

Full chord = $24$ units.

Common Pitfalls and Fixes

Mixing up radius and diameter: Always clarify if you’re being asked for the full width (diameter) or half (radius).
Wrong unit conversions: Double-check if you should be dividing or multiplying by 100 for cm↔m conversions.
Confusing triangle types: Look carefully at both angles and side lengths before deciding on a triangle’s classification.
Misapplying the Pythagorean theorem: Ensure the triangle is right-angled and identify the correct hypotenuse.
Area vs. Perimeter confusion: Area is space inside, perimeter is the distance around—don’t interchange their formulas.

Summary

The radius is always half the diameter in a circle, and tangents touch the circle at exactly one point, perpendicular to the radius.
Unit conversions between centimeters and meters require dividing or multiplying by 100.
Triangles can be classified by side length (equilateral, isosceles, scalene) and by angle (right, acute, obtuse).
For right triangles, use the Pythagorean theorem and area formula $\frac{1}{2}ab$ .
The perimeter of a rectangle is twice the sum of its length and width; the area is their product.
When in doubt, write out the relevant formula, substitute in variables first, then numbers; always check your units and your reasoning.