Foundational Geometry: Circles, Triangles & More!

Overview

Welcome to this deep dive into foundational geometry! In this session, you'll develop a clear, practical grasp of key geometric ideas: circles and their properties, converting units, classifying triangles by sides and angles, essential theorems (especially for right triangles), and calculating perimeter and area for basic shapes. By the end, you'll be able to recognize patterns, approach geometry problems with confidence, and avoid the most common errors.

Concept-by-Concept Deep Dive

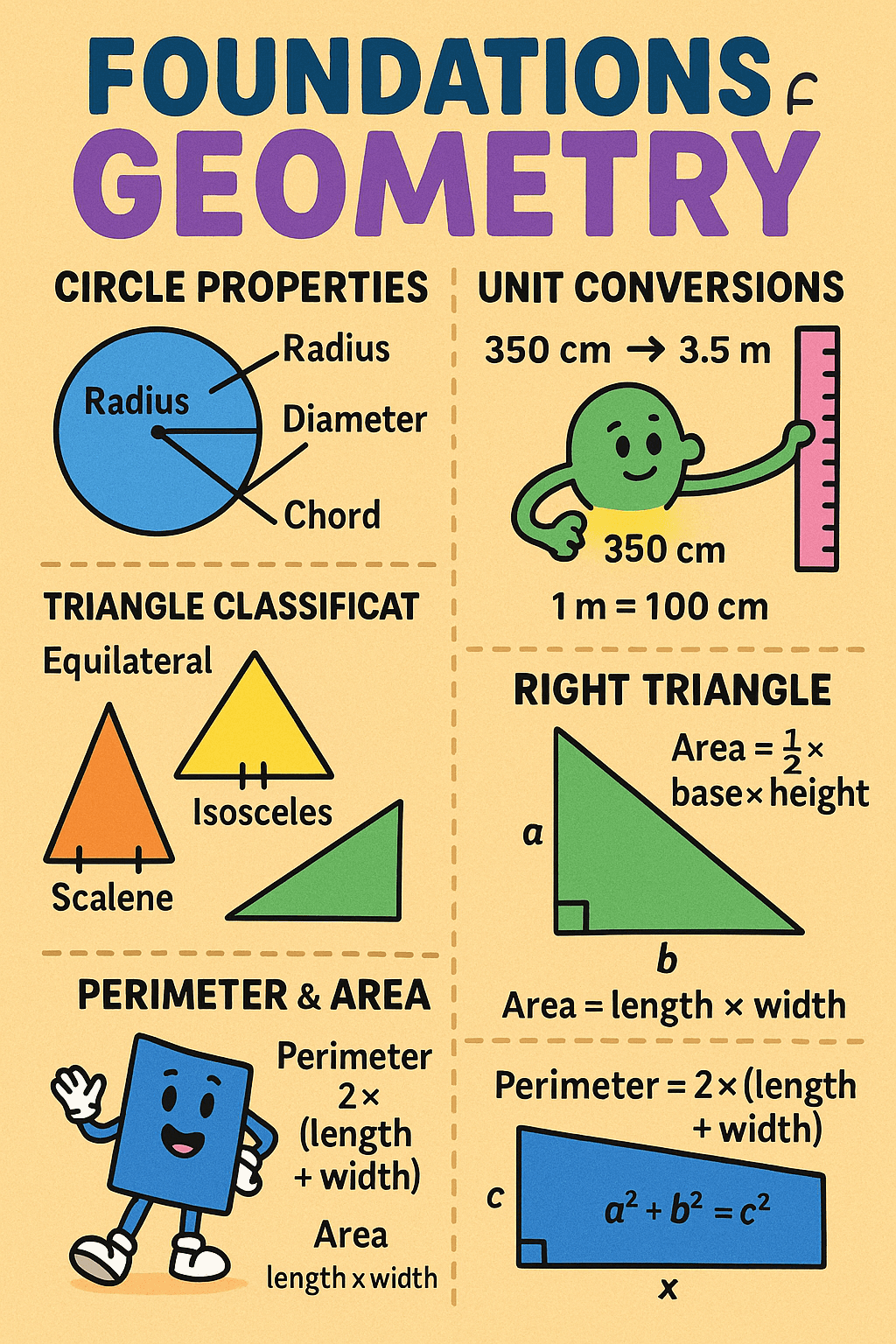
1. Circle Properties: Radius, Diameter, Tangent, and Chord

Circles are defined by all points equidistant from a center. Several core terms—radius, diameter, tangent, and chord—are essential for solving circle problems.

Radius and Diameter

• Radius is the distance from the center to any point on the circle.
• Diameter is a line passing through the center, touching two points on the circle—twice the radius.
• Conversion: If you know one, you can always find the other using the relationship: $$\text{Diameter} = 2 \times \text{Radius}$$ $$\text{Radius} = \frac{\text{Diameter}}{2}$$

Tangents

• A tangent is a straight line that touches a circle at exactly one point.
• Key property: At the point of contact, the tangent is always perpendicular to the radius drawn to that point.
• Common misconceptions: Some think a tangent can cross the circle, but it never does; it only touches at a single point.

Chord Length (not passing through the center)

• A chord is a straight line joining two points on a circle but not necessarily passing through the center.
• If you know the distance from the center to the chord (let's call it $d$) and the radius ($r$), you can use the Pythagorean Theorem: $$\text{Half chord length} = \sqrt{r^2 - d^2}$$ Then, double this to get the full chord length.

2. Unit Conversions

In geometry, measurements are often given in different units. A common task is converting centimeters (cm) to meters (m), or vice versa.

• 1 meter = 100 centimeters
• To convert from centimeters to meters, divide by 100.
• To convert from meters to centimeters, multiply by 100.
• Example: 350 cm = 3.5 m

Pitfall: Forgetting to divide or multiply by 100, or confusing which way to convert.

3. Triangle Classification and Properties

Triangles are classified by their angles and their side lengths.

By Angles

• Right triangle: One angle is exactly 90°.
• Acute triangle: All angles less than 90°.
• Obtuse triangle: One angle greater than 90°.
• Isosceles right triangle: Two angles are equal (45°, 45°, 90°).

By Sides

• Equilateral: All three sides equal.
• Isosceles: Two sides equal.
• Scalene: All sides of different lengths.

Area of a Triangle

• For a right triangle: $$\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$$
  • The two legs adjacent to the right angle serve as base and height.

Pythagorean Theorem

• Applies to right triangles: $$a^2 + b^2 = c^2$$ where $c$ is the hypotenuse.
• Use this to solve for an unknown side.

4.